题意简析
给出两棵树,每棵树有 \(n\) 个节点,求点对 \((x, y)\),使得下式最大化:
\[
\mathrm{deep}_x + \mathrm{deep}_y - \mathrm{deep}_{\mathrm{LCA}(x, y)} - \mathrm{deep'}_{\mathrm{LCA'}(x, y)}\]
\(n \le 366666\),边权可能为负。
思路解析
点分治/边分治 做法
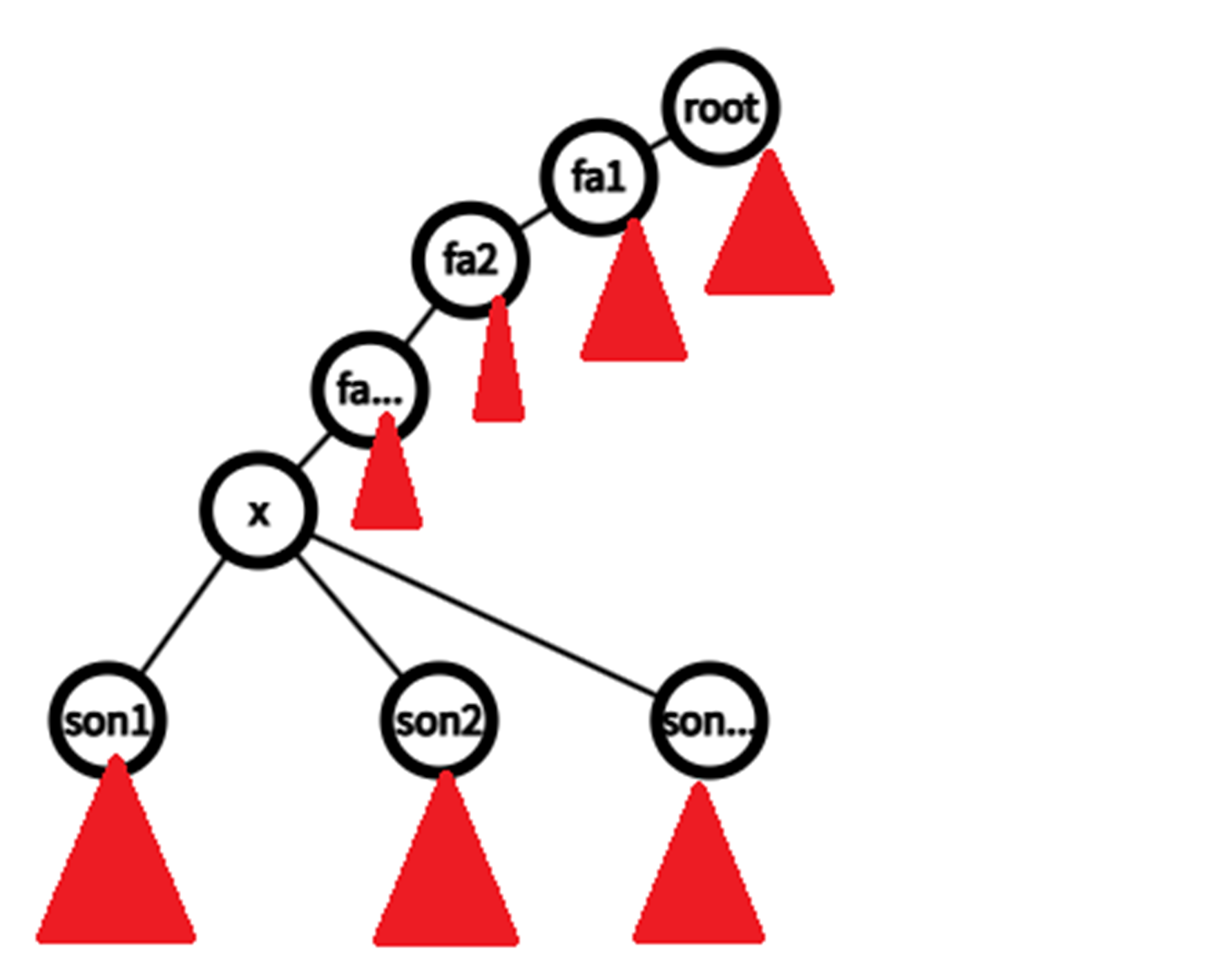
以点分治为例,在有根的情况下分治结构如上。设 \(root\) 为根节点,\(x\) 是当前的重心。
显然的,非 \(root\) 所在的其余子树 \(son_1,son_2,son_{\cdots}\) ,地位相等,正常合并。
对于 \(root\) 所在的部分,还需要分类讨论成 \(fa_1, fa_2,fa_{\cdots},root\) 这几种情况。
对于每个部分分别暴力统计,显然是会超时的。依据经验,做有根点分治/边分治题目时,要利用题目中的特殊性质。
- 利用 LCA 与另一个点无关的性质,将影响范围缩小到系数。
- 利用题目的特殊性质,将 \(root\) 所在的部分进行动态单点查询。
- 有根的关键点不在 LCA(与本题无关)
为简化思考过程,以使用边分治为例。
对于跨越了中心边的点对 \((x, y)\),假设 \(y\) 处于根所在的连通块,且处在局部根为 \(r\) 的部分。则题中所要求的量转化为:
\[\mathrm{deep}_r + \mathrm{deep}_y - \mathrm{deep}_{\mathrm{LCA}(r, y)} - \mathrm{deep}_{\mathrm{LCA}(x', y)}
\]
其中 \(x'\) 与 \(y\) 无关,于是可以把这部分贡献直接计算到 \(y\) 上。
现在所求的量为带点权的第二棵树上的 LCA 深度的最小值。仍然建立虚树进行树形 DP。时间复杂度 \(\mathcal{O}(n \log^2 n)\)。
但是如果我们不会写虚树呢?
树上启发式合并(dsu on tree)做法
我们可以有两种写法:
- 完全启发性合并,优点是十分短小精悍。(
其实是我点分治调了两年半) - 先树链剖分选出重儿子,再暴力枚举轻儿子进行合并,优点是不会拆除父亲所在的部分。
