无向图的必经边问题
问题:给定一张无向图,求点 \(S\) 到点 \(T\) 的所有路径中必须经过的边。
考虑到这个“必经边”一定是割边,我们很容易想到用 e-DCC 来解决这个问题。
分类讨论:
- 当 \(S\) 和 \(T\) 属于同一个 e-DCC 时,无必经边;
- 当 \(S\) 和 \(T\) 不属于同一个 e-DCC 但连通时,此时将 e-DCC 缩点后,两个 e-DCC 在缩点后形成的树上路径的边即为必经边(可看下图);
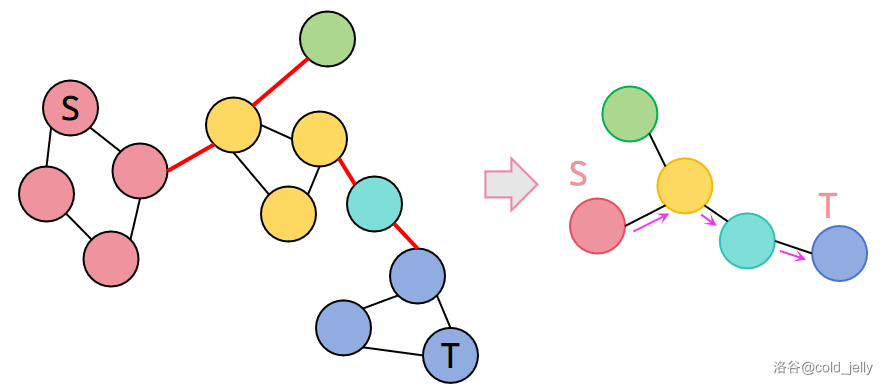
- 当 \(S\) 和 \(T\) 不连通时,无必经边。
例题:AcWing 397 逃不掉的路,求必经边的边数。
无向图的必经点问题
问题:给定一张无向图,求点 \(S\) 到点 \(T\) 的所有路径中必须经过的点。
必经点一定是割点,类似于求必经边,我们采用 v-DCC 来解决。
分类讨论:
- 当 \(S\) 和 \(T\) 属于同一个 v-DCC 时,无必经点;
- 当 \(S\) 和 \(T\) 不属于同一个 v-DCC 但连通时,此时将 v-DCC 缩点后,两个 v-DCC 在缩点后形成的树上路径经过的割点(缩点后的,不包括 v-DCC 内的割点)即为必经点;
- 当 \(S\) 和 \(T\) 不连通时,无必经点。
例题:P5058 [ZJOI2004] 嗅探器。
