管他什么DP来了做法都一样
确定状态定义->明确子问题->确定状态转换方程->找边界->打表验证
树形其实也就只是在树上跑DP而已
一般两种遍历顺序:
1.自上而下
2.自下而上
今天我们先来讨论讨论先是第一种情况:以自上而下的顺序跑DP
洛谷P1352 没有上司的舞会
这玩意是个经典的树形dp
确定状态定义:
每个职员要么来要么不来,两种状态我们很显然可以分开来维护:
设
f(i,0)为i职员不参加舞会时的最大快乐值
f(i,1)为i职员来参加舞会时的最大快乐值
明确子问题
很显然,某个职员来不来和他的上司来不来有着直接的关系嘛
所以说我们可以通过员工节点来维护他的上司节点
当某位员工的上司不来的时候他可以选择来或者不来
但要是上司来了,那这位员工可就不能来了
所以......
确定状态转化方程
f(i,1)表示i职员参加舞会的最大值,而他参加了他的下属就肯定不会再来参加
所以我们可以得到:
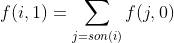
其中一条就出来了!
那看看该职员不来的情况呢?
当员工i不来参加时,他的下属可以选择来或者不来,而f维护的是最大快乐值
所以我们可以得到:

好的,这下完整的状态转移方程就解决啦!
确定边界条件
开头也说过,这道题是自下而上的遍历顺序
我们来好好分析一下
在确定状态转移方程的时候,我们知道了,f(i,0)和f(i,1)都是由他的员工,即他的孩子节点来维护的
要是某位员工没孩子(bushi)......
要是某位员工没有下属,即这位员工他是个树上的叶子节点呢?
那该员工来参加是的最大快乐值就只能是他自己的快乐值了,可怜的底层社畜......
综上,我们可以得到:
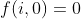 ,
, 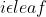
 ,
, 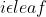
打表验证就不呈现出来啦,自己造一组数据手搓结果就行()
上代码
#include<bits/stdc++.h>
using namespace std;
//const int MAXN=1003;某人第一遍敲的时候RE原因实录...眼是真瞎...
const int MAXN=6005;
struct node
{int fa=0,r=0;bool leaf=0; //注意初始化vector<int> son;
}tr[MAXN];
int n,dp[MAXN][2],vis[MAXN],root;
void dfs(int v)
{vis[v]=1;if(tr[v].leaf)return;for(int w=0;w<tr[v].son.size();w++)if(!vis[tr[v].son[w]]) dfs(tr[v].son[w]);dp[v][1]=tr[v].r;dp[v][0]=0;int child; //加个中间量读起代码来好读一点() for(int i=0;i<tr[v].son.size();i++){child=tr[v].son[i];dp[v][1]+=dp[child][0];dp[v][0]+=max(dp[child][1],dp[child][0]);}return;
}
int main()
{int l,k;cin>>n;for(int i=1;i<=n;i++)cin>>tr[i].r;for(int i=1;i<=n-1;i++){cin>>l>>k;tr[l].fa=k;tr[k].son.emplace_back(l);}for(int i=1;i<=n;i++){ if(tr[i].fa==0) //查找根节点 root=i;if(tr[i].son.size()==0){tr[i].leaf=1;dp[i][0]=0;dp[i][1]=tr[i].r;}} dfs(root); //从根节点开始遍历cout<<max(dp[root][0],dp[root][1]);return 0;
}
简洁的结尾
